The Intuition of Slope in Linear Algebra

I know! I know! Exam time and holidays. Too much Halo lately. So here is a quick post on the concept of ‘slope’ that you have been hearing in the classes recently in the form of y = mx + c.

Well, I don’t see why it should be weird to understand. Let’s simplify things in this post.

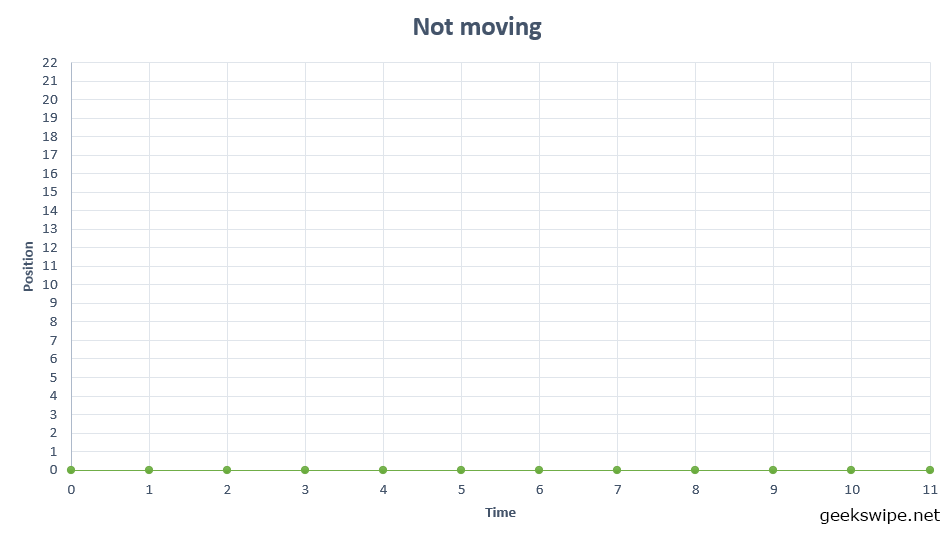
Imagine you are in a car and not moving. If you plot a graph with the y-axis as your position and x-axis as the time, you will have a straight line. Why? Because y is always 0 and the time runs on x-axis until the universe ends. And it will be a straight line.

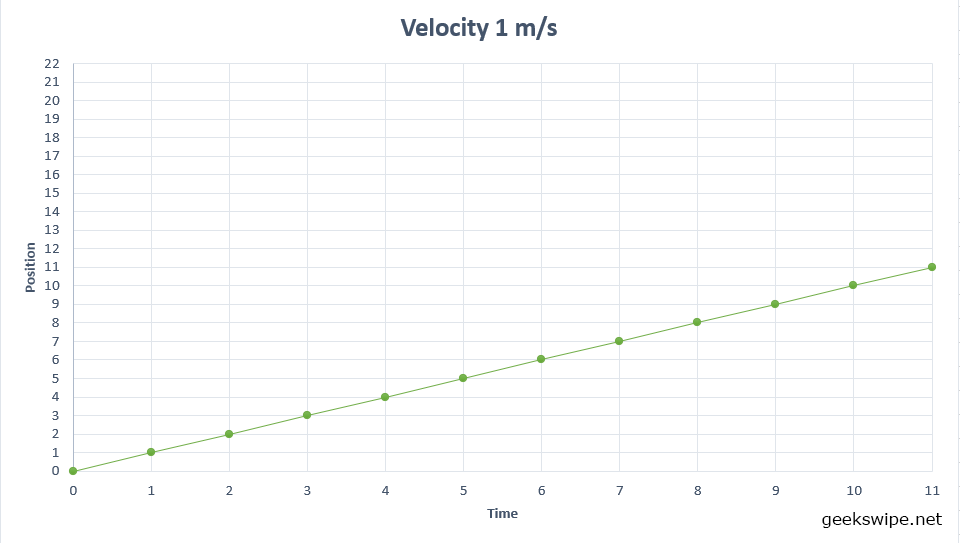
Lets reset the clock to 0. Now you start moving at 1 m/s velocity. And the time runs on the x-axis as your position rises in the y-axis. The graph will look like this. A straight, but inclined line.

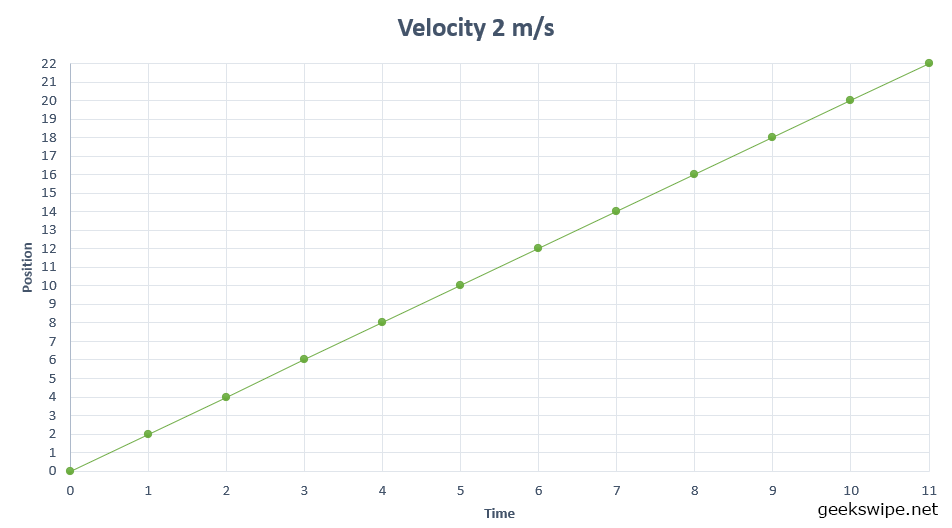
Now reset the clock to 0 and bring the car back to 0 again. This time you start moving at 2 m/s velocity. And the graph will look like this. Another straight line, but inclined even more compared to the 1 m/s line.

Intuitive explanation to slope

And now by intuition, the slope can be related to inclination as – ‘how inclined the line is that joins all the (x,y) coordinates of a linear equation’.

For our first case where the car did not move, the line is not inclined. So the slope is 0. ‘m’ is 0. Let’s substitute this in the equation.

y = mx + c.

y = 0 + c.

Wait! What is c? It is where the line meets the y-axis, so in our case, c is 0. It is where the line starts.

So there you go!

y = 0.

For the other two cases, the line is inclined upwards with a slope. Here the value of y rises as the value of x runs. And we know that the slope m is a positive value as the inclination is in the positive quadrant. But how do we find the slope value?

If you look at the graph, the relation between y and x is apparent. And the inclination of the line is determined by how fast y changes with x.

So if we can find the ratio of change in y to change in x for a given coordinate, we can determine the value of m.

• For the case of 1 m/s, the equation becomes, y = 1x + 0, which becomes y = x.
• For when the velocity was 2 m/s, the equation is y = 2x + 0, which is y = 2x.

So to simplify further and relate it to the textbook definitions, x is the run part. y is the rise part. And m is the ratio of change in y to change in x or like you have read, rise divided by run.

Why the slope is important?

Knowing the slope is important because it shows where the line is going and how fast the value of y is changing. If we could plot a line with given data in a graph, it is pretty easy to predict the intermediary and future values of y. In other words, slope is what predicts the position of your car numerically and graphically beyond the observed data points.

I hope this helps you understand. If you’d love to read more content like this, please send me an email and let me know.

This post was first published on April 6, 2006.