Why Hatches and Doorways in Ships and Airplanes Are Oval?

You might have skipped this as a trivial thing to analyze, but there had to be a time in your life where you must have wondered about the doorways and windows in an airplane, or a ship, or a submarine being oval and not the conventional way. Though you might argue that there are conventional doorways in ships, most of the main structural openings in ships, submarines and airplanes will only be round or oval like in the picture above.
The basics
For any material, like a steel bar at rest, there will always be internal forces fighting themselves to balance one another. When you look inside the steel bar with a hypothetical microscopic vision, you can visualize the molecular bonds from what you have learned from your schools. In a solid, these molecules hardly move around. They are so bonded to each other that when you try to rip the steel into two parts, the molecules at the top of steel bar hold hands together and won’t let go that easy, and the molecules below push each other so close. In other words, the top part of the steel bar experiences tension and the bottom part experiences compression. This tension or compression per unit cross-sectional area is what we technically refer as the tensile stress and compressive stress, respectively.
Holes and stresses
Okay! Stop bending it! You really can’t break it. Let’s carve out a nice little mouse hole in the steel bar, just like the one in the Tom and Jerry cartoons. What happens now? The force you need to apply to break the steel bar is quite reduced, yet still not close to breaking it into two. Take an identical steel bar and now make a wedge in it. Like a deep cut. Intuition tells that the bar could be easily broken with the sharp deep cut or a developing crack in it. This is because the stresses around the crack, a discontinuity, will be excessively high when compared to the stresses at the other areas without a hole or crack. In the case of the mouse hole cut, this is higher, and in the case of the wedge, the highest.
Here is a quick analysis that I did on two identical steel bars in CATIA, to help you visualize the concept of stress concentrations for the two discontinuities discussed above.
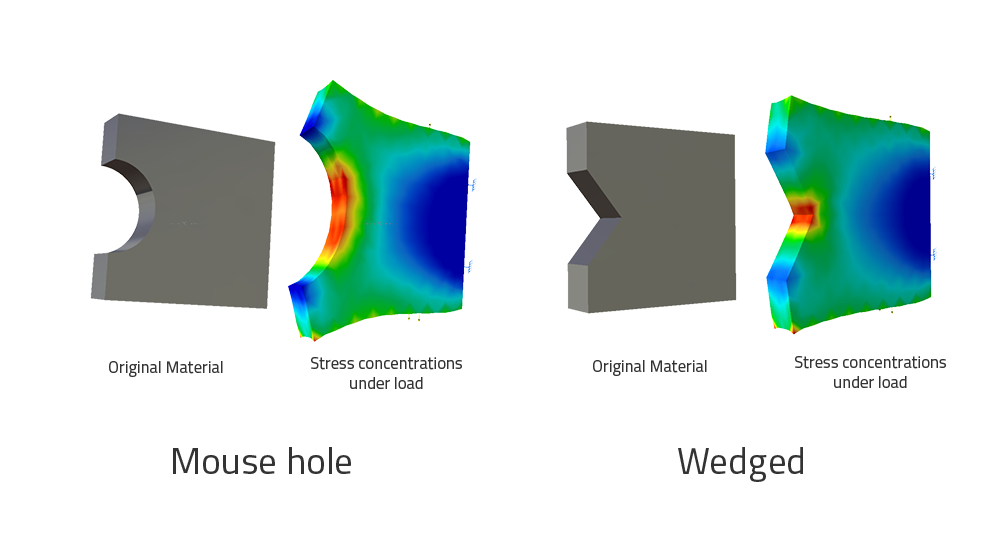
These red areas represent very high stress concentrations. Notice the stress concentration around the sharp tip on the right. It’s not quite distributed like the former blunt one on the left.
The maximum stress at such rounded and sharp cuts can be calculated with certain accuracy using the following formula derived by Charles E. Inglis. Though it is used for elliptical cracks, it is still accurate for our case.
\(\large \sigma_\text{max} = \sigma_\text{s} \left( 1 + 2 \sqrt{ \frac {L}{r} } \right)\)
Where \(\sigma_\text{s}\) is the stress, \(\text{L}\) is the length of the crack or cut from the surface of the material and \(\text{r}\) is the radius of the tip (the mouse hole cut has a radius while the crack has a negligible radius).
Doorways, windows, hatches are just big holes in a material
So if a crack in the steel bar makes it easier to bend or break the material, how should doorways, hatches in ships and windows in airplanes be designed? Indeed, by eliminating any sharp corners! As we have seen above, the sharp cuts and corners have more stresses concentrated around them. For sharp doorways, the radius of the curvature (the tip radius) is negligibly small and all that we have left in the formula above is the length of the doorway. As this is a complete hole unlike the semicircular mouse hole, the value of \(\text{L}\) is doubled, which is then multiplied by the existing stress in the material. As the value of \(\text{r}\) decreases (as the corners become sharper and sharper), the stresses at those particular points rise enormously, and would eventually exceed the strength (breaking stress) of the material and fail catastrophically. Therefore, to reduce these incidents, the corners are usually rounded, and hence the oval shape.
Check the following two animations that explain this concept visually. I did this analysis by clamping both ends and applying equal and opposite forces on both faces.

A sharp-cornered doorway

A round-cornered doorway
You could clearly see how the local stresses develop at the corners, and how the material behaves for both sharp and rounded corners. This pragmatically proves that rounded corners are structurally more beneficial than sharp corners. Besides this, the rounded corners also serve the purpose of adding sealing for water or airtight hatches with ease and a less probability of crack development, unlike a sharp corner. The next time you travel in an airplane or a ship, this could be a good topic to start a conversation.
This post was first published on January 14, 2016.








The first jet airliner, the DeHavilland Comet, taught us to round the corners of the windows on airliners. Because the altitude at which jet liners cruise is so much higher and and the liners have to be pressurized, the Comet experienced failures around the windows (and some other places as well). When they analyzed the information from the window failures, they figured out that the windows need to have rounded corners; if not be circular or oval. They learned a lot from the Comet. You should read about the Comet and all the problems encountered with the world’s first jet airliner.
Those GIFs are oddly satisfying. It feels… alive!
Nice to go with a simulation there. Thank you.
Nice. Thanks for explaining this. Have been wondering about this when I was on flight!