How Gyroscopes Work? – an Intuitive Explanation
The physics involved in Gyroscopes could be very hard to comprehend at times and could even seem so unbelievable. Despite it defying the gravity, it also defies our intuition. The underlying physics is rather very simple. Here is an intuitive way to understand how gyroscopes work.
Angular momentum and the right-hand rule
In order to understand the working of a gyroscope, we might need to brush up a little about angular momentum, which mostly is counter-intuitive to visualize. Fear not, it is quite easy to comprehend once you get through the hard part. I will try my best to describe it in an intuitive way.
In general, the angular momentum of a rotating body is represented as shown below.
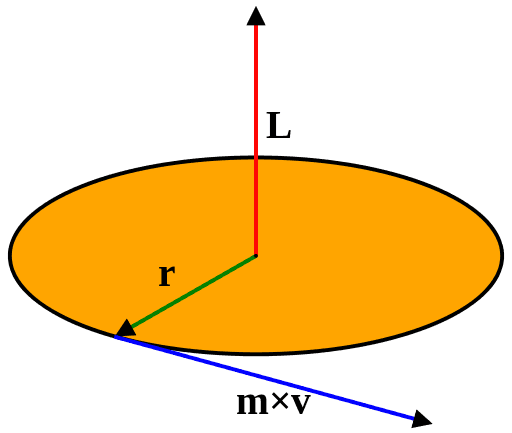
Where L is the angular momentum, r is the radius from the centre and m x v is the linear momentum of the object (m = point mass and v = linear velocity). I hope these are self-explanatory, except for the angular momentum’s (L) vector part (for most of you). Why is the angular momentum vector pointed upwards? Obviously, there is nothing acting in that direction. Still, why is it so?
Is it because of the actual physical direction of the object? Well, yes it is. The direction of the angular momentum changes at every instance as the object rotates. For a distributed mass like a wheel, the moment of inertia comes into play and we can visualize this much better. Consider yourself as a point somewhere in the outer rim, now when you look at the axis, you can tell which way you are rotating. We could either tell that you are rotating anti-clockwise or clockwise. How could we possibly communicate this? Humans agreed upon a rule to represent this in a simpler way and called it the right-hand rule. It’s quite simple to get the intuition too. Curl your hands in the direction of the rotation, if the spin is anti-clockwise as shown in the figure, then the direction of your thumb would be pointing upwards and vice versa. This is that simpler direction of the angular momentum vector or pseudovector, which will always be perpendicular to the plane of rotation.
Gyroscopes
Now, with a clear vision of angular momentum, let’s talk about a practical phenomenon observed with Gyroscope and find out why it seems to defy gravity. Let’s take the usual setup of a wheel attached to a string from the ceiling. It looks like the one shown below.
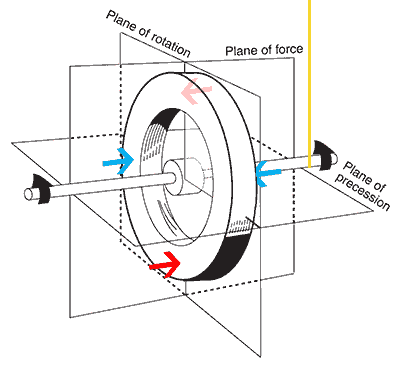
The right end is supported by the string (yellow). Assume that you are supporting the left end with your hand. When you take your hand off from the system, there will be a torque acting through the centre of mass. As the wheel begins to fall, the upper half of the wheel experiences a downward acceleration to the left and the lower half moves to the right and continues upwards. When you consider the whole system, this is just the torque caused by gravity, trying to do its job to rotate the whole setup. As gravity continues to pull down, the setup comes to rest eventually.
Gyroscopic precession
What happens if the wheel is already spinning? In that case, the torque would still be acting on the whole setup with the lever arm hinged to the string. Instead of rotating (falling) downwards due to the torque created by gravity, the setup rotates to the right, with the string as an axis of rotation (at the beginning). What the heck is this?
Well, here is the part where we don’t easily understand this gyroscopic precession. Let’s try understanding what happens.
Earlier, we’ve seen that the top half of the wheel (while not spinning) would experience a greater acceleration in the downward and left direction under the influence of the torque induced by gravity. When the wheel spins, this particular segment or point in the wheel begins to accelerate at the same time as it begins to move. The angular velocity increases. When the point completes the quadrant and reaches a ninety-degree angle from its initial position, the magnitude of the angular acceleration will be higher at that point. The same happens to the bottom-most point but in the opposite manner. The upward acceleration to the right would be at its maximum magnitude at a ninety-degree angle from its initial point. Now, the angular momentum of the whole wheel, due to these two accelerations, will be anti-clockwise when seen from the top. This rotates the wheel around the string axis.
Why does it defy gravity? Well, to fall down, there should be an acceleration downwards, right? We just saw that the acceleration is high at ninety-degree from the top and the bottom. When the two points further rotate, the remaining acceleration cancels out with the upcoming acceleration due to gravity in both the segments. So the net angular velocity is zero at the top and bottom points. This makes it look like the wheel is defying gravity.
So the grand finale. As the friction in the bearing slows down the rotation, the magnitude of the angular acceleration decreases and eventually the wheel begins to yield to the gravity. The torque slowly starts to rotate the axle and the wheel downwards.
With Right-hand rule
With the pseudovector notation, this becomes simple. The angular momentum vector of the whole system would be pointing outwards the plane of force. In addition to that, for the spinning wheel, the spin angular momentum vector would be pointed outwards to the left of the axle. The torque due to gravity will be pointed outwards from the plane of force. This torque is always perpendicular to the spin angular momentum. Torque is nothing but the change of angular momentum over time. So when the torque changes, the spin angular momentum changes too. This change makes the spin angular momentum to chase the torque vector, as they stay perpendicular all the time.
Will precession stop?
Of course, it will! A gyroscope (the wheel) precesses only because of the unbalanced torque induced by gravity. Therefore, if we could tie up another string to the left of our wheel, it would stop precessing. Nevertheless, I guess, you won’t need this explanation for that. The wheel will be rotating anyways if you have already constrained that degree of freedom. Indeed, this is what they actually do in gyroscopes such that it stays in the same orientation.
A great practical effect of this can be observed in the helicopter cyclic controls, which mostly are at ninety-degree phase.
This post was first published on November 23, 2015.











Is it just the bearing slowing down the wheel, or is the energy being used up faster by the load not being spread evenly through the bearing by the gravity acting through the turning point of the other end of the wheel?
I gave up trying to understand this because your language is so imprecise. For example: “As the wheel begins to fall, the first half of the wheel experiences a downward acceleration to the left and the lower half moves to the right and continues upwards”. What is the first half of the wheel? What is the lower half? What is left? What is right? Where am I relative to the wheel? What does this mean?
Hey! Thanks for the feedback.
But I am not sure which part is imprecise here. The description explains the figure. And the arrows in the figure clearly indicate the directions left and right. “Assume that you are supporting the left end with your hand”. This makes it clear about the directions as well. Did you follow the figure? Try to read again, following the figure this time if you have missed it. Hope this helps.
Update: The word ‘first half’ might have sounded vague. I have changed it to ‘upper half’.
The article is very good and informative . However you have not explained about the red and blue arrows which will be useful
Thanks
Can you explain why the effect of angular acceleration is maximum at 90 degrees?
Sure. As explained, in a spinning gyroscope, for any point on it, the magnitude of the angular acceleration (due to the torque created by gravity in this case) will be higher when that point completes a quadrant, which is at 90 degrees apart. So when the top point experiences the torque in the downward direction, it would have already been travelled away from that position, still accelerating. When it completes a quadrant, the torque would still be acting, but in a perpendicular direction, turning the gyro sideways.
You have no idea how much youtube videos I went through before I got here!
Me too! Veritasium had a nice video demonstration but lacked this type of basic explanation. After reading this it all made sense to me.
Thorough and well written explanation. Very useful. Thanks!
I am in college now and still vectors are confusing as hell! But gyroscope precession makes sense to me finally!
Good explanation!
After watching countless videos that could not explain this intuitively, I got here. Beautiful explanation! Clearly understood what is happening with gyroscopes. Thank you very much for explaining it eloquently!
Finally an explanation that makes sense! I felt stupid for not getting this concept throughout my college. This is an incredible explanation by far. Thanks!