How to Measure the Radius and Circumference of the Earth?

Wouldn’t it be awesome if you could measure the circumference and the radius of the earth right from your home? Just to be sure, you should not take the words ‘right from your home’ too literally. However, you can calculate it from your home with some basic tools, a friend’s help, and some reference data.

The greek way – 240 BC

The very first person to determine the circumference of the earth was Eratosthenes, in sometime around 240 BC. His method was so simple that he just used sticks and geometry (and a poor guy) to determine the circumference of the earth.

It all started when he was peacefully reading something at the library of Alexandria. He read that in a city, Syene, little far away from Alexandria, people observed something different on a particular day (summer solstice). At noon, the vertical columns did not cast any shadows at all. He further read about a deep well, which usually hid in the shadows every day, lightened up during that particular noon, as the sun appeared directly overhead (Syene/Aswan lies near the tropic of cancer) and its reflection was seen in the water.

For some reason (Curiosity, it is!), Eratosthenes wanted to explore further. At Alexandria, he reproduced the conditions on the same day, a year later. He found that his stick did cast a shadow at an angle of 7.2°, while columns at Syene cast no shadows at all. He intuitively confirmed that this could only happen if the earth was round. Being a mathematician, he applied simple geometry and extended an imaginary line from both the locations towards the center of the earth, forming an arc sector with an angle of 7.2°. He then only needed to find the distance (arc length) between Alexandria and Syene to determine the circumference of the entire circle (Earth). He simply paid a guy to measure that distance between the two cities for him.

The distance was found to be 800 km (No, the unit was not kilometers back then… It was stadia!).

\(\large \frac{Arc \ angle}{360°} = \frac {Arc \ Length}{Circumference \ of \ the \ circle}\)

It ended up that simple for Eratosthenes. With a very simple geometry and an intuitive mind, he calculated the circumference of the earth close enough to the modern values. Let’s follow his footsteps and do it with some twenty-first century touch.

Experiment

Requirements

Before I begin, understand that this is a fun experiment and we are going to do it with everyday objects (that includes the internet). To begin, all you need is a clear day, vertical stick, and a friend (or friends) far away from you, preferably on the same meridian.

Data Collection

Choose a day, say September 25, 2015, and a way to synchronize up with your friend. Besides, using a camera would be cool, as you can record it and do it in an accurate way with more data points for better results.

1. Measure your stick’s length and set it up vertically (use a plumb for accuracy) on a surface where you can measure the shadow length as time passes.
2. If you are about to record the whole process, a clock next to it would be helpful to plot your data for a computerized analysis (video tracker analysis, hence you don’t have to measure anything).
3. If you have decided not to record, all you have to do is to measure the length of the stick’s shadow exactly at noon or at one-hour intervals.

Calculation

Here are the two locations I chose for this experiment.
My Hometown, Annur – 11.23°N, 77.10°E
A Place in Russia that’s hard to pronounce. Let’s call it Russia – 61.20°N, 77.37°E

For my experiment, I am going to simulate the data, as I don’t have any friends living at 61.20°N now. You can download my data for your reference.

After plugging all the recorded data into an excel sheet, I got a cute plot like this.

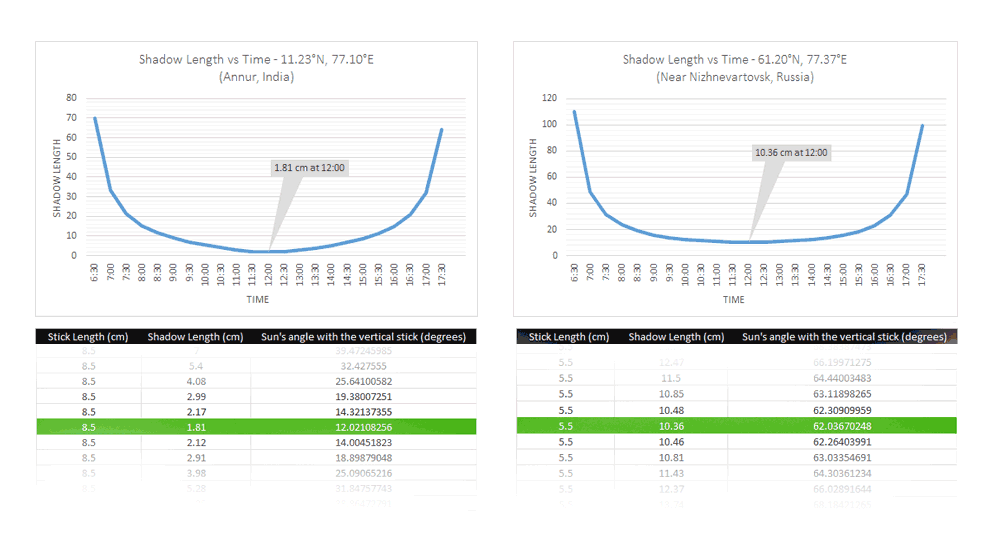
So now, I have the shadow length for different time sets. Let’s concentrate at the noon, where the shadows are the shortest for both the locations. With the shadow length and the actual length of the object, now I could get the angle that the sun rays make with the sticks at both the locations.

\(\phi = \arctan(\large \frac {shadow length}{stick length})\)

Let’s get to the drawing board and summarize the above calculations in a pictographic form. This is what I have calculated so far.

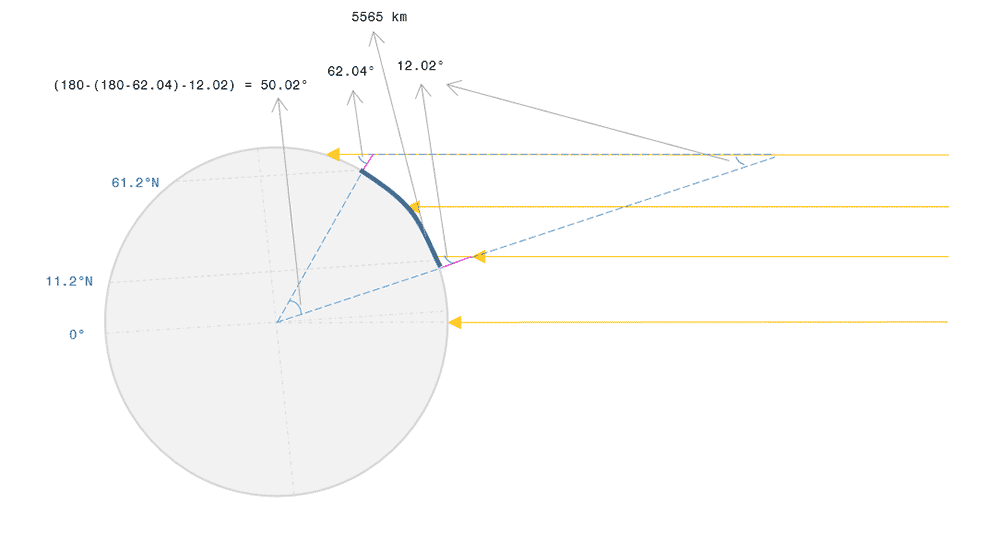
Approximate illustration of the sun ray angles and the position of the sticks on September 25, 2015. Not to scale.

If you look at the above pic, you could see the two latitudes of interest I’ve marked, and the two pink sticks stuck vertically (of course, not to scale!). When you extend an imaginary line vertically towards the center of the earth from both the sticks, they will meet exactly at the center, as we have assumed that the earth is a perfect sphere. Now, the angle of the sunlight to the stick would give you a latitude relative to the point on earth where the sun is directly overhead. However, the date is September 25 (missed the equinox by two days) and the sun is overhead somewhere at 0.61°S. So I simply extended the lines outward of my position to form a triangle and found out the angle between my place and Russia. All I need is the distance between the two locations. For this, I tried to hire actual humans, but it didn’t work out that good. So I sent a pigeon to the Russian location and found that the distance it took by air to reach the spot is 5525 km. Compensating for the terrain, I added up 40 km (Though, I assumed that the earth is a perfect sphere, this compensation could give me better results, as the earth is not a perfect sphere). Hence, the approximate distance would be 5565 km.

\(\large \frac{50.02°}{360°} = \frac {5565 \ km}{Circumference \ of \ the \ earth}\)

Circumference of the earth = 40055.48 km, which is 99.95% accurate.

Radius = 6375.02 km.

This feels awesome even with the data that I have simulated. I would actually like to do it with some friends soon and try something challenging like finding the longitude too. Latitude is actually easy to find if you have an almanac by your side. Looking up at the almanac, I have the sun’s declination for September 25 as 0.61° due south. Subtracting this from my position’s 12.02° angle, I get 11.41°, which is close enough to my actual latitude 11.23° (33km apart). Incase if I had it in a different longitude, I’d have compared the noon with the Greenwich meridian’s and found out the local noon. The difference would give me my longitude. It’s that simple.

Now, go find friends across the globe and start your experiments.

This post was first published on September 27, 2015.