I am oversimplifying this for the sake of explanation. According to relativity, any two observers in the universe who are in inertial frames must always agree about the speed of light. Always! Because it is proven to be constant in all conditions!
If you and your friend have two light clocks (A light clock measures time-based on the ticks of a light beam that’s bounced between two mirrors A and B) each and are on the ground, the time measured with those two clocks will be in sync. Of course! Because you both are in the same inertial frame and the time it takes for the light to bounced off the mirrors in your clocks will be the same.
But now let’s put you and your clock on a spaceship that can travel at half the speed of light. The spaceship now is travelling at 1/2 c and you are in it, watching the light beam bounce between A and B vertically. Everything is normal for you.
But when you fly past your friend, who is looking at you from the ground. He would see weird things happening in your clock. The light beams of your clock will not appear to travel vertically. He’d observe that the light beam in your clock takes a diagonal path (in the direction of the spaceship) as it bounces from B to A or A to B.
It is obvious that he observes it this way because the spaceship is moving too fast and the mirrors are moving along with the spaceship too. So the light’s path would be diagonal for ANY observer.
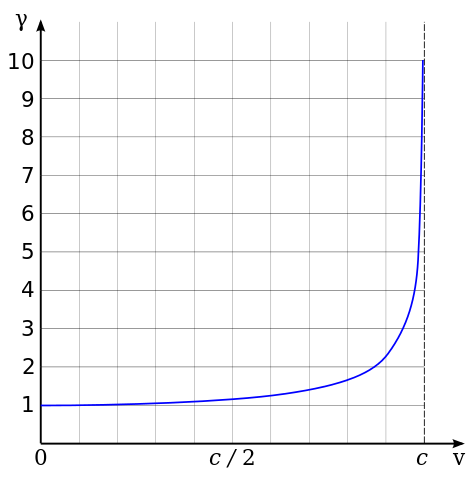
The light beam as it appears to take a diagonal path, it also appears that it has to take a longer distance to cover. Due to this longer distance, the light clock in motion now ticks slower. Therefore time in the spaceship appears to be slower for your friend. This is known as time dilation.
But for you, inside the spaceship, everything will be normal. And if you happen to observe your friend, it would appear that he is moving at 1/2 of c speed relative to you and you will observe his clock to be slower too.
Now let’s talk about ageing in the context of special relativity!
Say if you use that spaceship to travel to Proxima Centauri which is 4.2 light-years from Earth. You will be travelling at 1/2 the speed of light and it would take you 8.4 years to reach the star and another 8.4 years to come back to the Earth.
For you, the time passed is all normal – 8.4 back and forth, so 16.8 years of your life has passed. But on Earth, as time is relative, the people on Earth would’ve experienced a different time, that would have ticked faster than yours — and hence they would be a few years older than you.

To have a significant change in the time delta, you’d need to be travelling above 75% of the speed of light.